日常生活の中には様々な解決するべき問題が存在していますが、特に工学分野においては、その多くは最適化問題という形になっています。
最適化問題とは、与えられた条件の下でなるべく良い解を見つけるという問題であり、これを解くには様々な方法があります。
　数理計画法（数理最適化）は、最適化問題を解決するための一つの手法です。
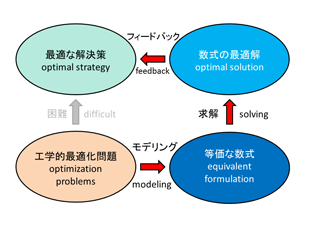
　数理計画法では、まず解くべき最適化問題を数理的にモデル化・定式化し、得られた数式を解くことにより問題の最適解を得る、という解決法をとります。
　問題を数式の形で表すというアプローチは、他の経験的な最適化手法と数理計画法の最も異なる部分であり、これにより真の最適解を求めるという点が数理計画法の強みとなっています。
　数理計画法の適用範囲は分野横断的であり、スケジューリング、ロジスティクス、マーケティング、ネットワークなど様々な分野に適用可能です。

We encounter a wide variety of optimization problems in daily life, especially in technology-related problems.
The aim of optimization is to find the best solution under given constraints; various approaches are available for solving optimization problems.
     In the field of mathematical programming, one first describes an optimization problem to solve in a form of mathematical equations, and then finds the solution for the modeled equations so as to obtain an optimal solution for the orginal problem.
     Although computer simulation making use of heuristic procedures is quite popular, it does not guarantee attainment of an optimal solution and provide no information about the accuracy of generated solutions.
On the other hand, mathematical programming techniques unable us to obtain a true optimal solution, and gives outcomes with benefits that will flow back to enrich our society.
     Methods of mathematical programming are multidisciplinary; these procedures can tackle versatile problems, such as scheduling, logistics, marketing, network systems, etc.